C › C언어의 구조체와 RBTree(Week5_Day2)

게시 2024/08/02

By 정재욱

20 분읽는 시간

오늘 C언어를 이용한 스택, 큐, 이진트리의 구현을 해보면서 구조체의 선언과 메모리 할당에 대해 새로 이해한 내용을 정리하려한다.

구조체 정의

  
typedef struct _queue
{
	QueueNode *head;
	QueueNode *tail;
} Queue;

이런 식으로 _queue라는 구조체를 선언을 하였으며, 별명을 Queue로 하였다.

구조체의 정의는 컴파일러에게

Queue라는 구조체는 이
크기(16바이트)를 가지면서,
멤버로 head, tail포인터를 가지고 있어.
얘는 메모리 상에 이런식으로 배치가 될거야.
라는 것을 알려주는 행위 이다.

정의만으로 실제로 스택에 인스턴스화가 되지는 않지만, 나중에 이렇게 쓸거야~ 를 알려주는 것이다.

그럼 이후 런타임 시간에 메모리의 할당 등이 일어나면서 사용을 하는 것이다.

런타임 시간에는 구조체에 대한 정보를 알고 있지 않다.
컴파일러가 구조체를 보고서 정해놓은 레이아웃을 사용하는 것이다.

구조체의 선언

이제 특정 함수에서 구조체를 사용하는 경우에 대해 알아보겠다.

구조체 변수로서 사용할 때
1 Queue queue;
이렇게 선언을 했다면 queue는 Queue 자료형의 변수로서 스택에 구조체가 인스턴스 화가 된다.
스택은 메모리의 할당과 해제를 자동으로 관리한다.
queue.head, queue.tail 로 구조체의 멤버를 사용하려면 먼저 초기화를 해주어야 한다.
현재 상태에서는 각 포인터에 접근을 하게 될 경우 쓰레기 값을 가지고 있기 때문에 최악의 경우 segment fault가 발생하지 않아 찾지 못하는 버그를 유발하게 된다.
때문에 NULL로 초기화를 해주고 사용을 하는 것이다.
NULL로 초기화 되지 않은 포인터를 사용할 경우 우연히 민감한 정보에 접근이 가능할 수도 있다.
구조체 포인터로서 사용할 때
1 Queue *queue;
이렇게 선언을 하게 되면 우리는 Queue라는 구조체를 가리킬 수 있는 queue라는 포인터를 선언한 것이다.
때문에 쓰레기 값을 가리키고 있는 포인터 하나를 선언한 것이지 우리가 의도한 대로는 사용할 수 없는 상태이다.
이 때는 malloc을 사용하여 동적으로 메모리 공간(힙)을 할당 해 주어야 한다.
1 Queue *queue = (Queue *)malloc(sizeof(Queue));
이 때, malloc이 반환하는 void* 은 암시적으로 해당 포인터 타입으로 변환이 되지만, (Queue *) 이라는 명시적인 형 변환으로 컴파일러와 다른 코드를 읽는 사람에게 해당 타입임을 알려주는 것이 좋다.
저렇게 malloc을 사용하게 되면 Queue 구조체를 담을 수 있는(Queue의 크기만큼 = 16 바이트) 비어있는 빈 공간을 할당받게 된다.
이 때 중요한 점은 저 공간은 구조체를 담을 수 있는 빈 공간 이라는 것이다.
여기서의 빈 공간은 무조건 비어있다는 것은 아니다.
여기서 부터 여기까지 너써~ 한 것이 때문에 다른 값이 들어있을 수도 있다.
여기서 앞서 짚고 간 개념이 등장한다.
컴파일러는 우리의 구조체가 어떠한 형이고, 크기이고, 멤버는 누구이고, 메모리 공간에 어떻게 배치할 지를 알고 있다.
그렇기 때문에 이후 우리가
1 2 3 Queue *queue = (Queue *)malloc(sizeof(Queue)); queue->head = NULL; queue->tail = NULL;
로 각 멤버 포인터들을 초기화 할 때에 빈 공간이였음에도 아 여기에 head포인터를(8바이트) 저장하고 얘는 NULL을 가리키는 구나!(tail도 마찬가지)가 가능한 것이다.
또한 이 경우 free를 통해 사용후에는 메모리 해제를 해주며 메모리 누수를 방지해야 한다.(힙은 사용자가 임의로 할당, 해제하는 공간)

RB tree

RB tree의 정의

레드블랙트리(Red-Black Tree)는 이진탐색트리의 한 종류로 스스로 균형을 잡는 트리이다.

균형(Balance) : BST의 경우 모든 노드가 한쪽으로 치우치는 worst case가 발생하는 단점(O(n))이 있다.
이걸 방지하기 위해 스스로 균형을 맞추며 삽입, 삭제, 검색이 O(logn)이 될 수 있도록 한다.

RB tree의 속성

모든 노드는 Red 혹은 Black 이다.
루트 노드는 Black 이다.
모든 nil(leaf) 노드는 Black 이다.
nil 노드 :

RB tree에서만 쓰는 특별한 개념.
존재하지 않음을 의미하는 노드로 자녀가 없을 때 자녀를 nil노드로 표기 한다.
RB tree에서는 이 nil노드를 값이 있는 노드와 동등하게 취급한다.
때문에 RB tree에서는 leaf 노드는 nil 노드 이다.
Red 노드의 자녀들은 Black 이다(Red가 연속적으로 존재할 수 없다).
임의의 노드에서 자손 nil 노드들까지 가는 경로 상의 Black 수는 같다(자신은 제외).
Black height :
특정 노드에서 임의의 자손 nil 노드까지 내려가는 경로 상의 Black 수(자신은 제외).
5번 속성을 만족 할 경우에만 성립하는 개념.
색을 바꾸면서 5번 속성 유지하기.

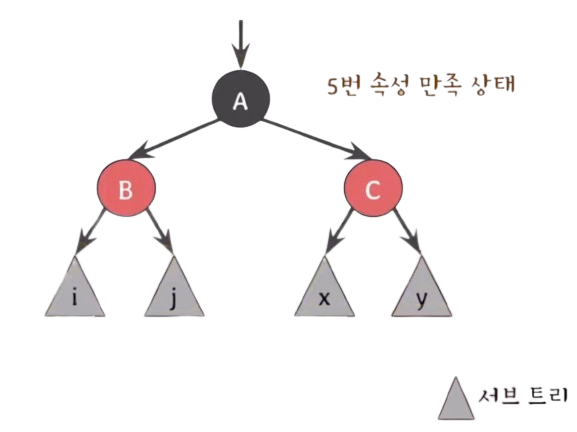
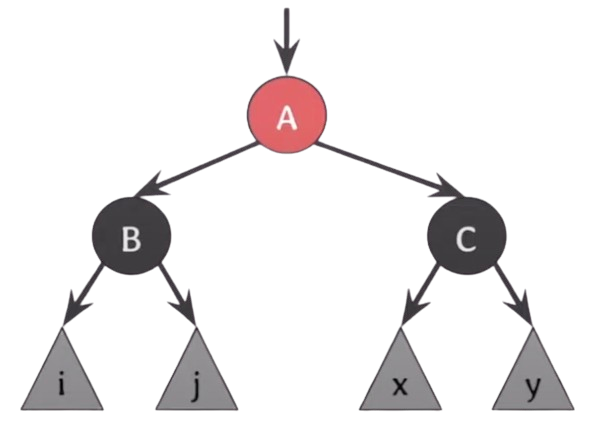
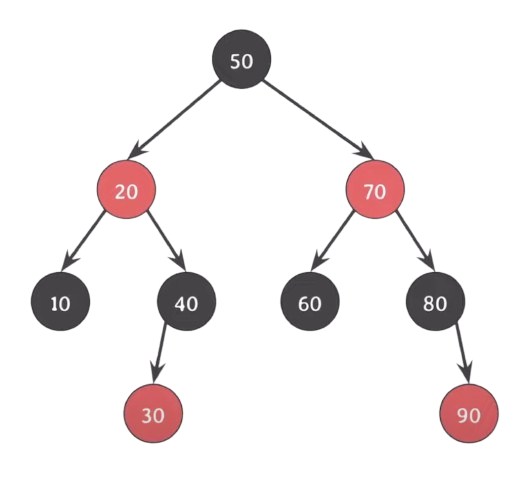
RB tree가 5번 속성을 만족하고, 두 자녀가 같은 색을 가질 때, 부모와 두 자녀의 색을 바꿔줘도 여전히 만족한다.
그림을 보면 부모의 입장에서 부모와 자녀의 색을 바꿨음에도 Black의 수가 하나 늘어나긴 했지만 모두 black height가 같음을 알 수 있다.
자식의 입장에서 또는 서브트리의 입장에서는 달라진 것이 없다.

RB tree 의 균형

삽입 :
일반적인 BST와 동일하며, 삽입 후 속성의 위반 여부를 확인하고 재조정하여 다시 속성을 만족하도록 만든다.
삽입하는 노드의 색은 무조건 Red 이다.
삽입하는 노드가 Red여야 하는 이유 :
삽입을 한 이후에도 5번 속성을 만족하기 위해서 Red로 하는 것.
- 2번 속성을 만족하지 않을 경우 : 색을 Black으로 바꾼다.
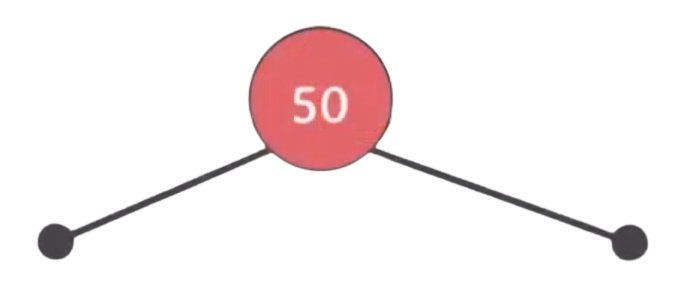
  사진과 같이 삽입하는 노드는 Red이며, 자동으로 nil노드(무조건 Black)가 달린다(3번 속성을 만족).
  만약 루트노드라면 2번 속성을 위반하기 때문에 색을 Black으로 바꿔주면 모든 속성을 만족한다.
- 4번 속성을 만족하지 않을 경우:
  - Case.3 :
    
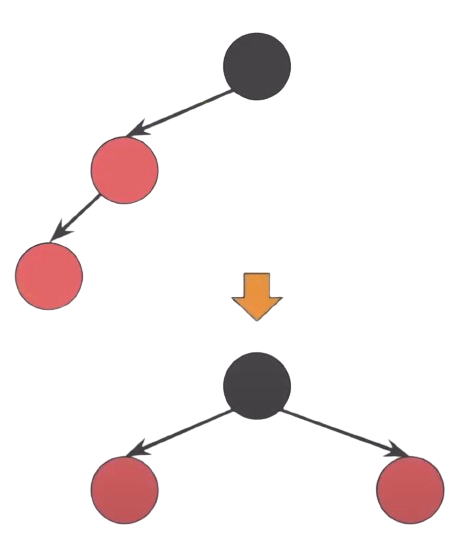
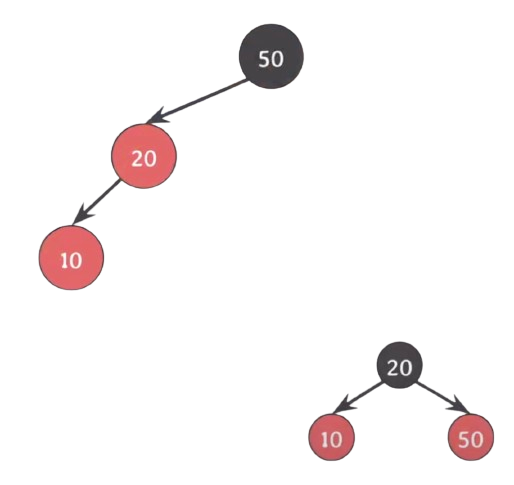
    이런 식으로 red가 한 쪽으로 몰려 버렸을 경우(4번 속성 위반) 구조를 바꾸면서도 BST의 특징을 유지시키려면 회전을 시켜야 한다.
    1. 20과 50의 색을 바꿔준다.
    2. 50을 기준으로 오른쪽으로 회전한다.
    삽입 된 Red 노드가 부모의 왼쪽(오른쪽) 자녀이며, 부모도 Red이고 할아버지의 왼쪽(오른쪽) 자녀이며, 삼촌(부모의 형제)는 Black이라면(위 그림과 같다면)
    부모와 할아버지의 색을 바꾼 후 할아버지 기준 오른쪽(왼쪽)으로 회전한다.
  - Case.2 :
    
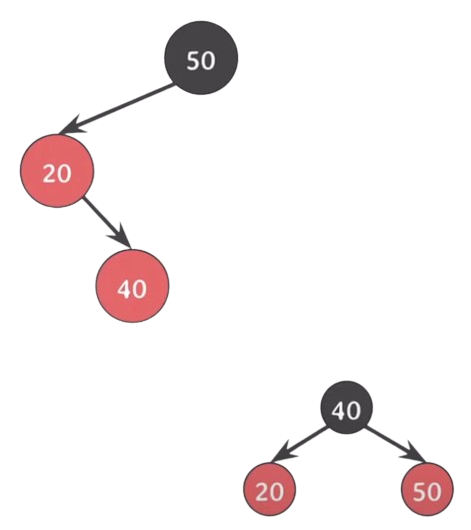
    Case.3와 다른 점은 삽입 된 노드를 기준으로 할아버지까지의 경로가 꺾였다는 점이다.
    그렇다면 꺾인 부분을 펴서 Case.3와 같이 해결하면 되겠네 ???
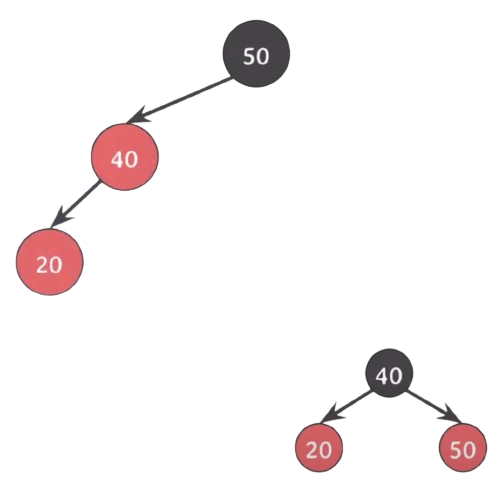
    1. 20을 기준으로 왼쪽으로 회전한다(이제 Case.3).
    2. 40과 50의 색을 바꾼다.
    3. 50을 기준으로 오른쪽으로 회전한다.
    삽입 된 Red 노드가 부모의 오른쪽(왼쪽) 자녀이며, 부모도 Red이고 할아버지의 왼쪽(오른쪽) 자녀, 삼촌은 Black이라면(위 그림과 같다면)
    부모를 기준으로 왼쪽으로 회전한 뒤 Case.3와 같이 해결.
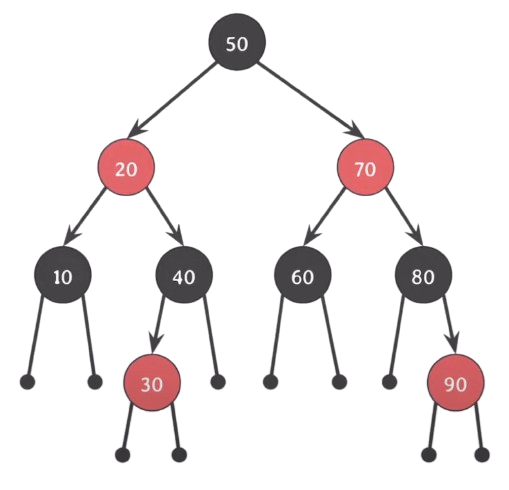
  - Case.1 :
    
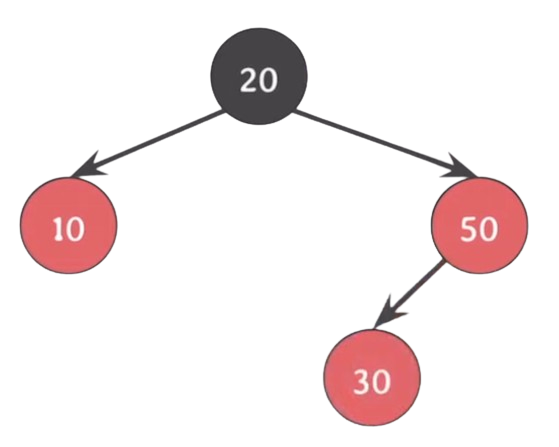
    이 경우에는 4번 속성을 위반하는 건 같지만, Red가 한 쪽으로 몰려있지 않다.
    4번 속성을 만족하면서 5번 속성도 만족시키기 위해서는
    RB tree가 5번 속성을 만족하고, 두 자녀가 같은 색을 가질 때, 부모와 두 자녀의 색을 바꿔줘도 여전히 만족한다.
    를 이용한다.
    1. 10과 50을 Black으로 바꾸고, 20을 Red로 바꾼다.
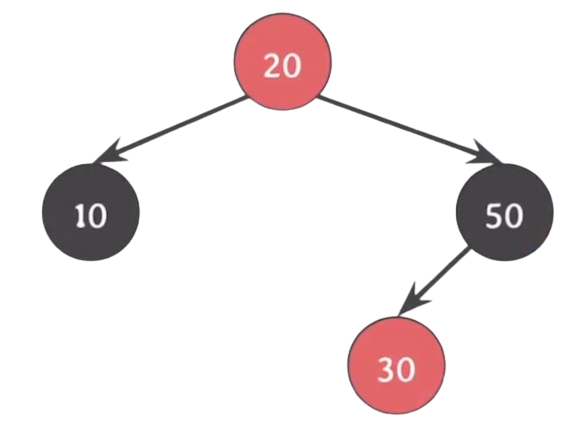
    2. 루트노드가 Red가 되어버려 2번 속성을 위반한다.-> 20을 Black으로 바꾼다.
      
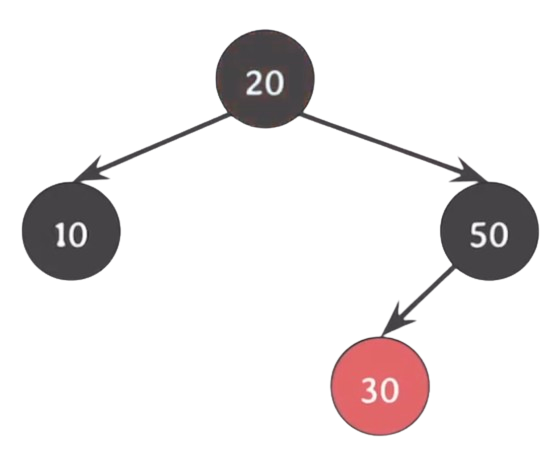
      그럼 이제 모든 속성을 만족한다.
    삽입된 Red노드의 부모도 Red, 삼촌도 Red이면(위 그림과 같다면), 부모와 삼촌을 Black으로 바꾸고 할아버지를 Red로 바꾼 뒤 할아버지에서 다시 확인(Root 이거나, 할아버지의 부모도 Red)한다.
삭제 :
일반적인 BST와 동일하며, 삭제 후 속성의 위반 여부를 확인하고 재조정하여 다시 속성을 만족하도록 만든다.
노드를 삭제할 때 어떤 색이 삭제 되는지가 속성 위반 여부를 확인하는데 중요!
삭제하려는 노드의 자녀의 수(유효한 값을 가지는 자녀)를 먼저 따져본다.
- 자녀가 없거나 하나일 때 : 삭제되는 색은 삭제 된 노드의 색.
- 자녀가 둘일 경우 : 삭제되는 색은 삭제되는 노드의 successor(오른쪽 서브트리의 가장 작은 값)의 색.
이제 삭제되는 색을 따져보자.
- Red가 삭제될 때 : 어떠한 속성도 위반하지 않는다.
- Black이 삭제될 때 : 2, 4, 5번 속성이 위반 될 수 있다.
  - 2번 속성이 위반 : 루트 노드를 그냥 검은색으로 바꿔주면 된다.
  위 같은 특수한 경우가 아니라면 항상 5번 속성을 위반하게 된다(Black의 수를 세리는데 Black을 지워버렸으니 당연).
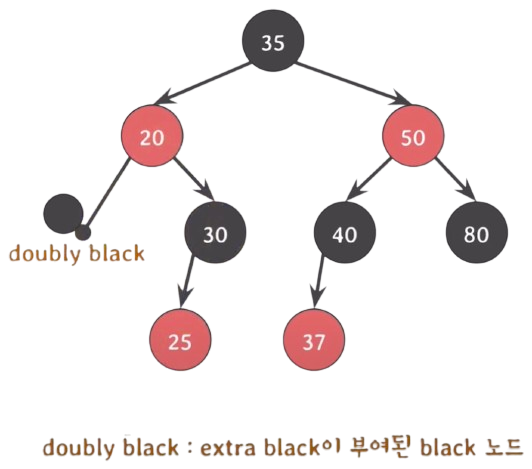
  - 5번 속성이 위반 : 삭제 된 색의 위치를 대체한 노드에 extra black을 부여한다.
    extra black : black height를 계산할 때 하나의 black으로 카운트 된다.
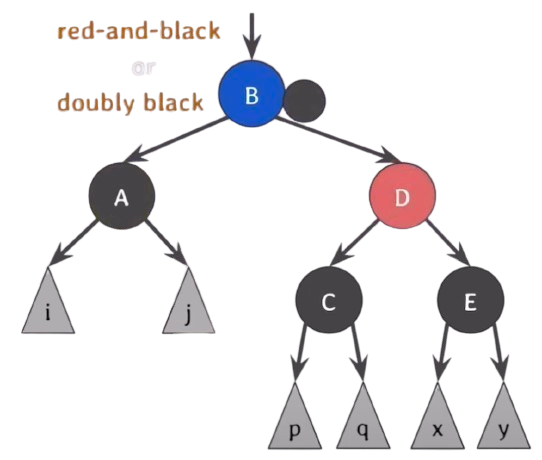
    doubly black : extra black이 부여된 black 노드.
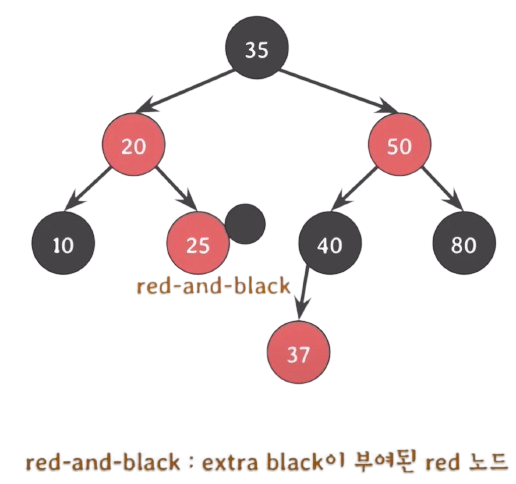
    red and black : extra black이 부여된 red 노드.
    red and black의 경우는 그냥 black으로 바꿔버리면 모든 게 해결이 된다.
    하지만 doubly black의 경우는 extra black을 어떻게 없앨 것인지가 관건이다.
    이에 4가지 경우가 존재한다.
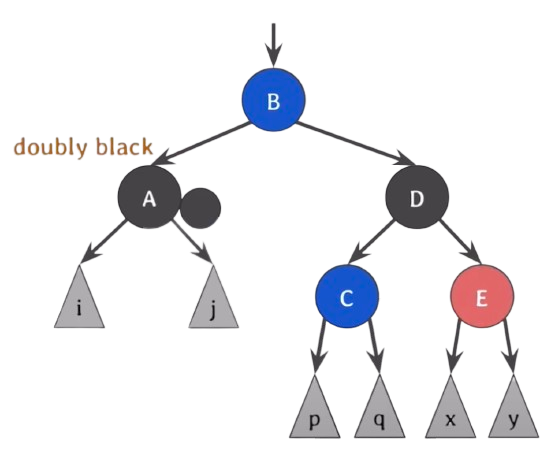
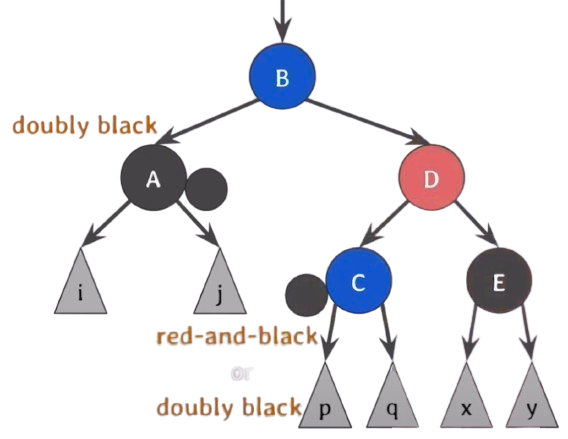
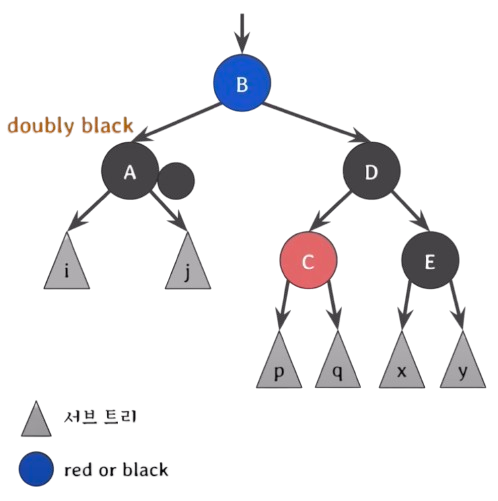
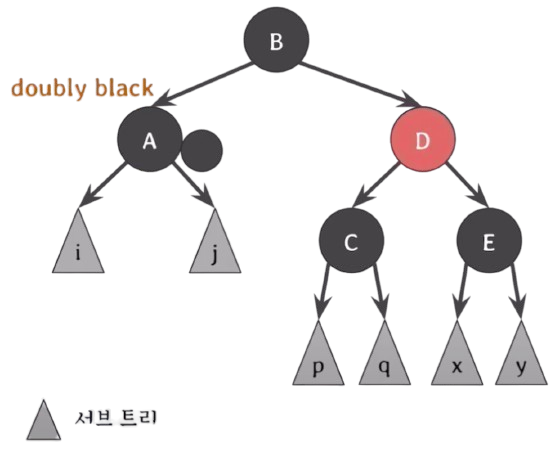
    - doubly black의 오른쪽(왼쪽) 형제가 black이고, 그 형제의 오른쪽(왼쪽) 자녀가 red일 때(Case.4) :
      c, b는 red일 수도 있고, black 일 수도 있다. 둘이 색이 같다는 뜻이 아니다.
      red를 왼쪽으로 doubly black의 위로 옮겨서 extra black을 주고 red and black을 그냥 black으로 바꾸면 되지 않을까???
      RB tree가 5번 속성을 만족하고, 두 자녀가 같은 색을 가질 때, 부모와 두 자녀의 색을 바꿔줘도 여전히 만족한다는 5번 속성의 특징을 응용해 보자!
      D를 자식과 색을 바꾸는 것이다. 근데 이 때 c가 red인지 black인지 모르기 때문에 extra black을 준다(5번 속성을 여전히 만족).
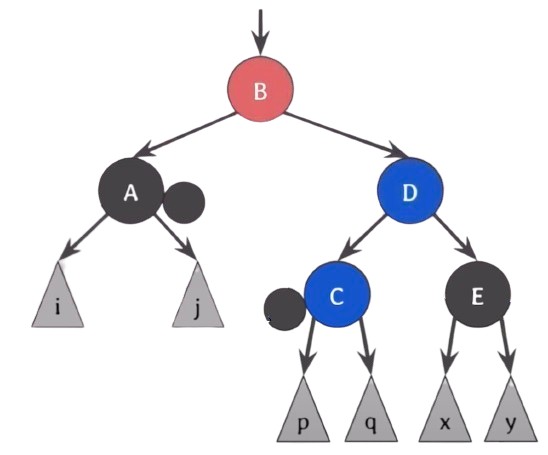
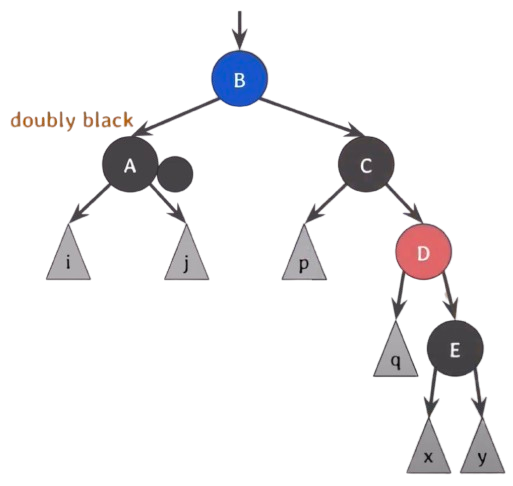
      이제 왼쪽으로 넘겨주고 싶은데, BST의 특징을 그대로 유지해야 하기 때문에 회전을 사용해야 한다.
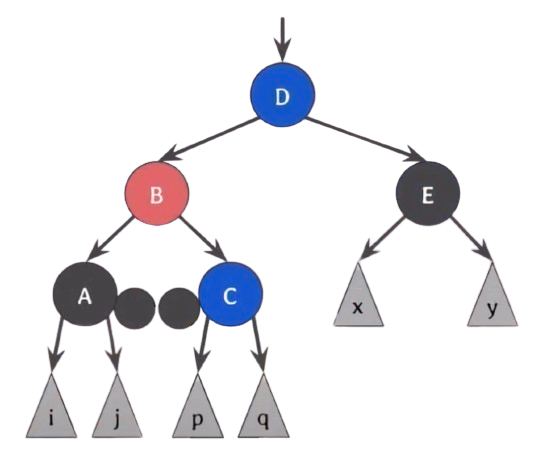
      회전을 하기 전에 먼저 red가 왼쪽으로 넘어갈 수 있도록 B와 D의 색을 바꿔준다.
      이제 B를 기준으로 왼쪽으로 회전을 시켜 준다.
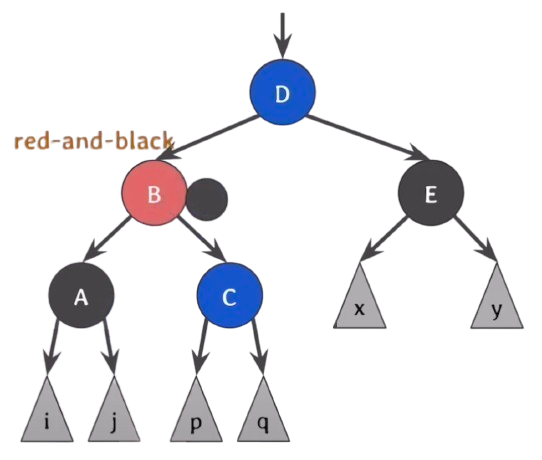
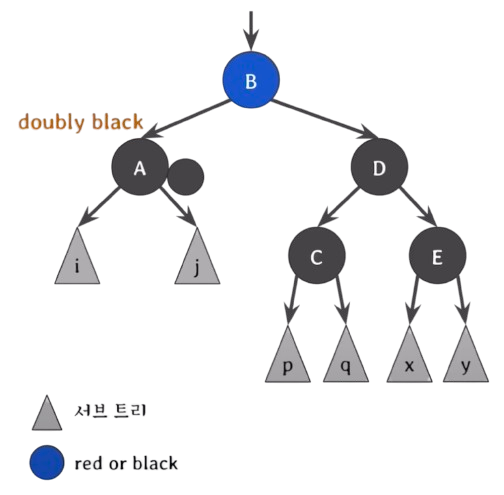
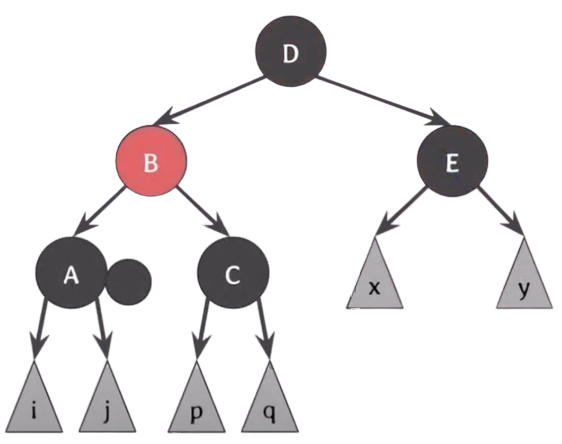
      이제 A, C의 extra black을 B로 올려서 red and black으로 만든 후 black으로 바꿔버리면 해결이 된다.
      이걸 이제 결론적으로 정리를 하면,
      오른쪽(왼쪽) 형제는 부모의 색으로, 오른쪽(왼쪽) 형제의 오른쪽(왼쪽) 자녀는 black으로, 부모는 black으로 바꾼 후에 부모를 기준으로 왼쪽(오른쪽)으로 회전한다.
    - doubly black의 오른쪽(왼쪽) 형제가 black이고, 그 형제의 왼쪽(오른쪽) 자녀가 red일 때, 그 형제의 오른쪽 자녀는 black일 때(Case.3) :
      Red를 오른쪽 형제로 옮겨 줄 수 있으면 Case.4로 생각하고 풀 수 있겠구나!
      doubly black의 형제의 오른쪽(왼쪽) 자녀를 Red가 되게 만들어서 Case.4를 적용하여 해결한다.
    - doubly black의 형제가 black이고, 그 형제의 두 자녀 모두 black일 때(Case.2) :
      extra black과 형제의 black을 모아서 부모에게 전달.
      그림 상 D는 red가 되는 것이다.
      결론적으로 doubly black과 그 형제의 black을 모아서 부모에게 전달해서 부모가 extra black을 해결하도록 위임(red and black일 경우 black으로 바꾸면 해결, doubly black일 경우 루트 노드이면 black으로, 아닐경우 case1, 2, 3, 4 중 하나로 해결 한다.
    - doubly black의 형제가 red이고, 그 형제의 두 자녀 모두 black일 때(Case.1) :
      doubly black의 형제를 black으로 만든 후 case 2, 3, 4 중 하나로 해결하면 되겠다!
      그렇게 하기 위해서는 B를 기준으로 왼쪽(오른쪽)으로 회전을 하면 되겠다!
      근데 5번 속성을 계속 만족해야 하기 때문에 B, D의 색을 미리 바꿔주고 회전을 하자!
      그럼 이제 doubly black의 형제가 black이 됬기 때문에 case 2, 3, 4 중 하나로 해결이 가능하다.