PYTHON › DP와 그리디(Week3_Day4)

게시 2024/07/22

By 정재욱

11 분읽는 시간

오늘은 3주차 알고리즘에 대해 정리 해보았다.

DP(동적 계획법)

DP란

동적 계획법이라는 이름은 뭔가 와닿지 않아 찾아보니 모 교수님께서 기억하기 알고리즘이라고 표현하셨다고 한다. 그렇게 표현한 이유는 DP알고리즘의 목적은 메모리를 사용하여(자료구조, 배열을 사용) 중복연산을 줄이고 수행속도를 개선하는 것이기 때문이다. 즉 한 번 수행한 연산을 기억하여 많은 경우의 수를 따질 때 반복을 하지 않아 수행시간을 줄이는 것이다.

DP 구분법

DP인지 구분 하는 법은

DFS, BFS로 풀 수 있지만 경우의 수가 너무 많은 경우.
완전 탐색의 마지노선은 대략 $5 * 10^6$ 이라고 생각.
그 경우의 수들에 중복연산이 많은 경우.

메모이제이션(Memoization)?

앞에서 말했듯이 한 번 수행한 연산을 기억하는 행위를 메모이제이션이라고 한다.’

DP 문제풀이 방식

DP의 문제 풀이방식은 Bottom-up 방식과 Top-down 방식 두 가지가 있다.

Bottom-Up(Tabulation 방식) Bottom-Up 방식은 작은 부분문제부터 해결하여 전체 문제를 해결하는 방식. 반복문을 사용하여 반복적으로 부분문제들을 해결하고 결과를 배열 등에 저장.
Top-Down(Memoization 방식) Top-Down 방식은 큰 문제를 작은 부분문제로 나누어 해결하는 방식. 재귀함수를 사용하여 문제를 작은 부분문제들로 쪼개고, 중복계산을 피하기 위해 Memoization을 사용.

DP식 사고방식

DP식 사고방식은

어떻게 하면 현재까지의 연산을 다시하지 않지?
어떤 정보를 남겨야 하지?
여태까지의 최적의 답을 쌓아간다는 생각!

보통 문제를 풀 때는 바로 수식을 찾으려고 하기보단 처음 몇 개 정도는 손으로 써보고, 규칙을 발견하면 그 때 수식화 하는 순서로 푸는 것이 좋음.

그리디 알고리즘(탐욕 알고리즘)

그리디 알고리즘이란

미래를 생각하지 않고 오직 현재 시점에서 가장 좋은 선택만을 하는 기법. 현재의 최선이 미래 전체의 최선은 아니기 때문에 최적해를 찾는 알고리즘은 아님. 그래서 근사 알고리즘 이라고 부르기도 함. 일상생활에서는 항상 최적해를 요구하지 않기 때문에 수행시간을 줄이기 위해 자주 사용함. 하지만 코딩 테스트를 풀어야하는 입장에서는 최적해가 보장되는 상황에서만 써야 함.

최적해가 보장 되는 조건

Greedy Choice Property 현재의 선택이 미래의 선택에 영향을 주지 않아야 한다.
Optimal Substructure 문제의 부분의 최적해가 모이면 전체의 최적해가 되어야 한다.

그리디 알고리즘의 풀이방법

풀이 방법의 핵심은 정렬이다. 어떻게 정렬해야 미래의 선택은 따지지 않고 현재만 고려해도 최적해를 구할 수 있을까?를 고민하면서 풀면 된다.

그리디 알고리즘을 사용하는 이유

수행시간이 짧으니까!

완전탐색을 하면 시간이 너무 오래걸려서 DP를 사용했는데 그리디 알고리즘은 이것 보다도 수행시간이 더 짧아!

LCS

LCS란

LCS는 두 가지 경우가 있다.

Longest Common Substring(최장공통문자열)
Longest Common Subsequence(최장공통부분수열)

둘 다 공통되면서 가장 긴 경우를 찾는건 맞지만, 큰 차이점이 하나 있다. 부분수열의 경우 건너뛰면서 가장 긴 공통 부분문자열을 찾지만, 부분문자열의 경우 한 번에 이어진 문자열을 찾아야 한다. 실제로 코드를 구현할 때는 코드 자체에 엄청난 차이를 가져오지는 않지만 구상하는 단계에서는 이점을 꼭 주의해야 한다.

LCS의 접근방법

Longest Common Substring(최장공통문자열)

$X = [x_{1}, x_{2}, \cdot\cdot\cdot\cdot\cdot\cdot\cdot\,, x_{m}]$

$Y = [y_{1}, y_{2}, \cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\,,y_{n}]$

$Z = LCS(X, Y) = [z_{1}, z_{2}, \cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\,,z_{k}]$

라고 생각하겠다. 물론 각 배열의 길이는 다 다르다.

Brute-Force 일단 무식하게 박아본다.
의외로 문제를 이해하는데 도움이 된다.
X의 모든 부분 수열 중에서 Y의 부분 수열인 것들의 길이를 구하고, 그 중에서 최대값을 찾는다.
당연하게도 지수 시간 복잡도를 가지게 되니 이건 불가능하다.

재귀 DP를 적용하기 전에 먼저 재귀적 관계를 파악해보자.

만약 $X, Y$의 마지막 원소가 같다고 하면

$x_{m} = y_{n}$ 일 때

$z_{k} = x_{m} = y_{n}$ 가 된다.

그럼 $Z_{k-1} = LCS(X_{m-1}, Y_{n-1})$ 가 성립한다.

만약 $X, Y$의 마지막 원소가 같지 않다면

$x_{m} != y_{n}$ 일 때 그럼 두 가지 경우로 나뉘게 된다. - $z_{k} != x_{m-1}$ 이면 $Z = LCS(X_{m-1}, Y_{n})$ - $z_{k} != y_{n-1}$ 이면 $Z = LCS(X_{m}, Y_{n-1})$

이제 재귀적으로 정의 해보게 되면,

$c(i, j)$ : 수열 $X_{i}, Y_{j}$의 $LCS$의 길이.

종료조건 : $i=0$ 또는 $j=0$이면 $c(i, j)=0$

재귀조건 :
  - $x_{i} = y_{j}$ 이면
  $c(i, j) = c(i-1, j-1) + 1$
  - $x_{i} != y_{j}$ 이면
  $c(i, j) = max(c(i, j-1), c(i-1, j))$
  ![](https://velog.velcdn.com/images/jju6924/post/368656bf-7519-4ce9-81c9-219e5f98a869/image.png)

고로 이런 함수를 만들 수 있다.

하지만 이렇게 재귀로 풀게 되면

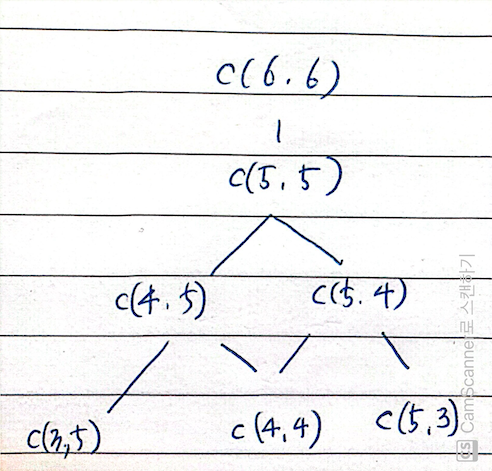아래로 풀어나가다가 c(4, 4)를 두 번 계산하게 되는 중복부분문제(Overlapping Subproblem)이 발생한다.

이 수행시간 단축을 위해 Top-down이 아닌 Bottom-up 구조로 풀어볼 수 있다.

```python
def lcs(x, y):
    x, y = [" "] + x, [" "] + y
    m, n = len(x), len(y)
    c = [[0 for _ in range(n)] for _ in range(m)]
    b = [[0 for _ in range(n)] for _ in range(m)]
    for i in range(1, m):
        for j in range(1, n):
            if x[i] == y[j]:
                c[i][j] = c[i - 1][j - 1] + 1
                b[i][j] = 1
            else:
                c[i][j] = max(c[i][j - 1], c[i - 1][j])
                b[i][j] = 2 if max(c(i, j - 1), c(i - 1, j)) else 3
    return c, b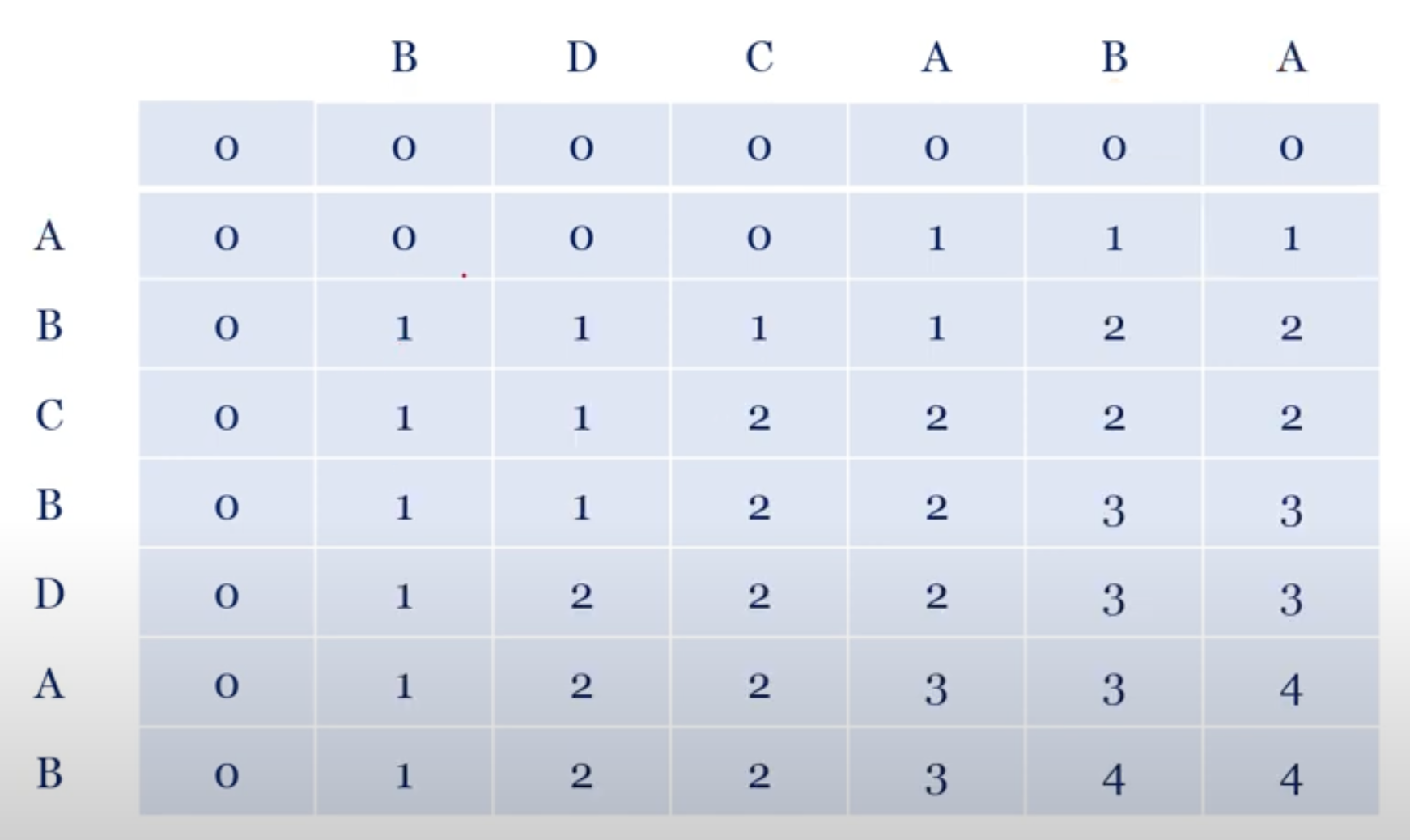
```
![](https://velog.velcdn.com/images/jju6924/post/51fe7b92-7e71-4f47-8f4a-9d0e3df0573e/image.png)

```python
def get_lcs(i, j, b, x):
    if i == 0 or j == 0:
        return ""
    else:
        if b[i][j] == 1:
            return get_lcs(i - 1, j - 1, b, x) + x[1]
        elif b[i][j] == 2:
            return get_lcs(i, j - 1, b, x)
        elif b[i][j] == 3:
            return get_lcs(i - 1, j, b, x)
```
c 행렬의 제일 마지막 원소가 곧 LCS의 길이가 되는 것이다.

그리고 LCS의 값을 구하기 위해 b행렬을 새로 사용했는데, 이 방법 뿐 아니라 c행렬의 마지막 원소에서 왼쪽과 위를 비교하며 같을 경우에는 진행하고 왼쪽 위 모두 같은 원소가 없을 때는 현재위치의 $x[i]$ 또는 $y[j]$ 를 출력하고,대각선으로 이동하는 방식으로도 구할 수 있다.